Cosine Similarity and connection to Machine Learning

Cosine Similarity is just an intimidating and mathmatical term for analyzing how two vectors are similar. If we remember the unit circle from high school, we remember a few things:

• The closer the cosine is to 1, the smaller the angle between the vectors
• When cosine is 0, the vectors are perpendicular
• When cosine is -1, the vectors are opposite

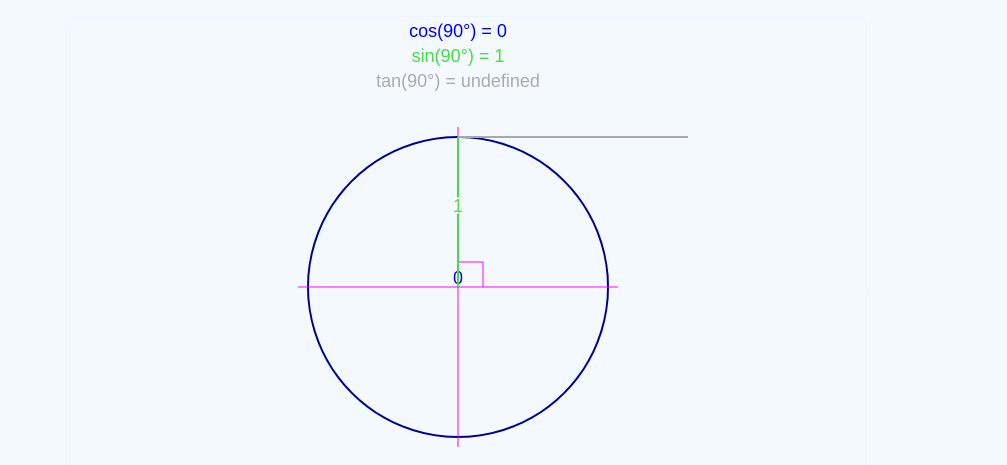
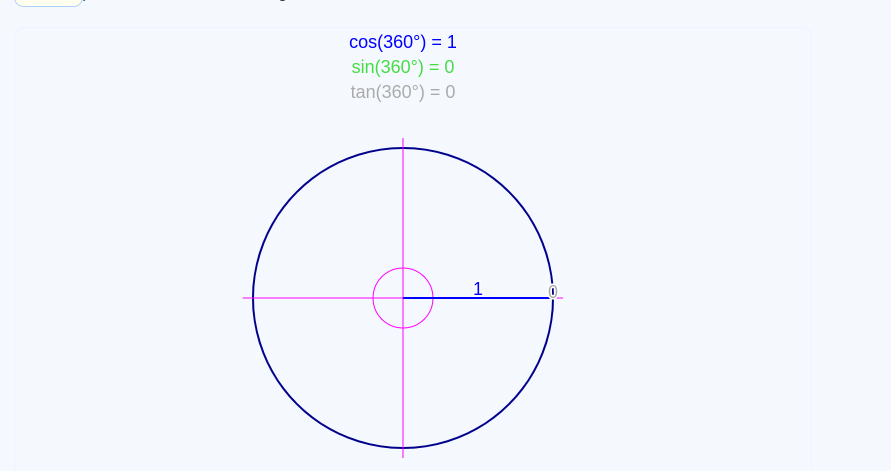
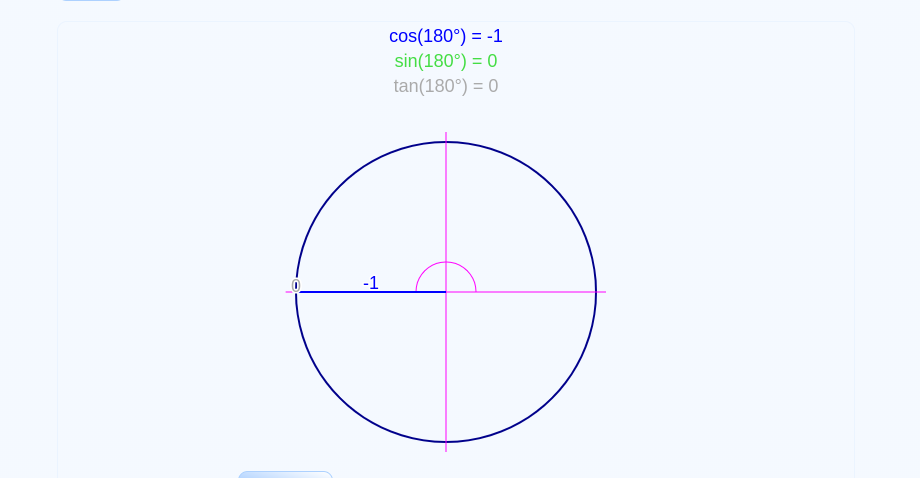
If we can represent sentences using vectors, we now have an interesting way to analyze how similar two sentences are to each other in natural language process. This leads us to us a more useful and computational use for the cosine similarity. To perform cosine similarity, we need to be able to get the magnitude of a vector and the dot product of two vectors.

Enter the magnitude and the dot product

Fundamentally, the magnitude of a vector is the length of a vector while the dot product is taking a vector and projecting it onto another vector. Mathematically, here are the way to get these. The Magnitude of the vector is just the square root of the sum of all of the components of a vector or

$\begin{Vmatrix} A \end{Vmatrix} = \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2...} $

The Dot Product of two vectors is multiplying the corresponding components of the vectors together and then adding the products. Notice that because we're multiplying corresponding components, we need the vectors to be the same length. Also, because we're getting a number from the dot product of these vectors, it only makes sense to get the dot product between two vectors at a time. Both of these constraints will become important when we try to analyze the similarity of two sentences.

$\vec{A} \cdot \vec{B} = a_1 b_1 + a_2 b_2 + a_3 b_3 $

With these two operations in mind, we can mathematically get the Cosine Similarity

$\cos{\theta} = \frac{\vec{A} \cdot \vec{B}}{\begin{Vmatrix} A \end{Vmatrix}\begin{Vmatrix} B \end{Vmatrix}}$

Examples

Let's assume that we have the following two vectors

$\vec{A} = <1,2,3,4>$

$\vec{B} = <5,6,7,8>$

Let's start with vector A and find the magnitude

$\vec{A} = <1,2,3,4>$

To get the magnitude, what we first want to do is to get every component squared so

$(1)^2 = 1$

$(2)^2 = 4$

$(3)^2 = 9$

$(4)^2 = 16$

Now all we do is to just put the square root house over the sum of all those squared numbers

$= \sqrt{1+4+9+16}$

$= \sqrt{30}$

Don't worry about actually calculating the square root right now (it doesn't come out to a pretty number anyway). We're going to use it in a larger calculation anyway so for now we'll just remember that

$\begin{Vmatrix} A \end{Vmatrix} = \sqrt{30} $

Now we'll do the same for vector B

$\vec{B} = <5,6,7,8>$

$\sqrt{(5)^2+(6)^2+(7)^2+(8)^2}$

$\sqrt{25+36+49+64}$

$\sqrt{174}$

Again, just leave the square root the way that it is for right now.

Now, let's get the dot product of these two vectors. Remember what the numbers in the vector were. We can think of it like we're laying the two vectors on top of each other and then just multiplying the top number by the bottom number where they line up.

$\vec{A} = <1,2,3,4>$

$\vec{B} = <5,6,7,8>$

$\vec{A} \cdot \vec{B} = (1)(5) + (2)(6) + (3)(7) + (4)(8) $

1 times 5 is 5, 2 times 6 is 12, 3 times 7 is 21, and 4 times 8 is 32

$ = 5 + 12 + 21 + 32 $

Now all we do is just add all of these together

$ = 70$

So this now gives us the dot product

$\vec{A} \cdot \vec{B} = 70 $

So now we can plug all of these numbers, the magnitudes of both vectors and our dot product, into our formula for the cosine similarity

$\cos{\theta} = \frac{\vec{A} \cdot \vec{B}}{\begin{Vmatrix} A \end{Vmatrix}\begin{Vmatrix} B \end{Vmatrix}}$

$\cos{\theta} = \frac{70}{(\sqrt{30})(\sqrt{174})}$

So now notice that the denominator is two square roots multiplied together, we can simplify that by just multiplying the numbers inside of the square roots and then just using the square root of that product. So 30 times 174 is 5220. So this means that we can simplify our about cosine similarity to

$\cos{\theta} = \frac{70}{\sqrt{5220}}$

Now is the time to break out the calculator and to get an approximation. The wavy equals sign below is a sign that we're taking an approximate value

$\cos{\theta} \approx .96886 $

If you were to plot this on a graph, you would see that the angle is very small

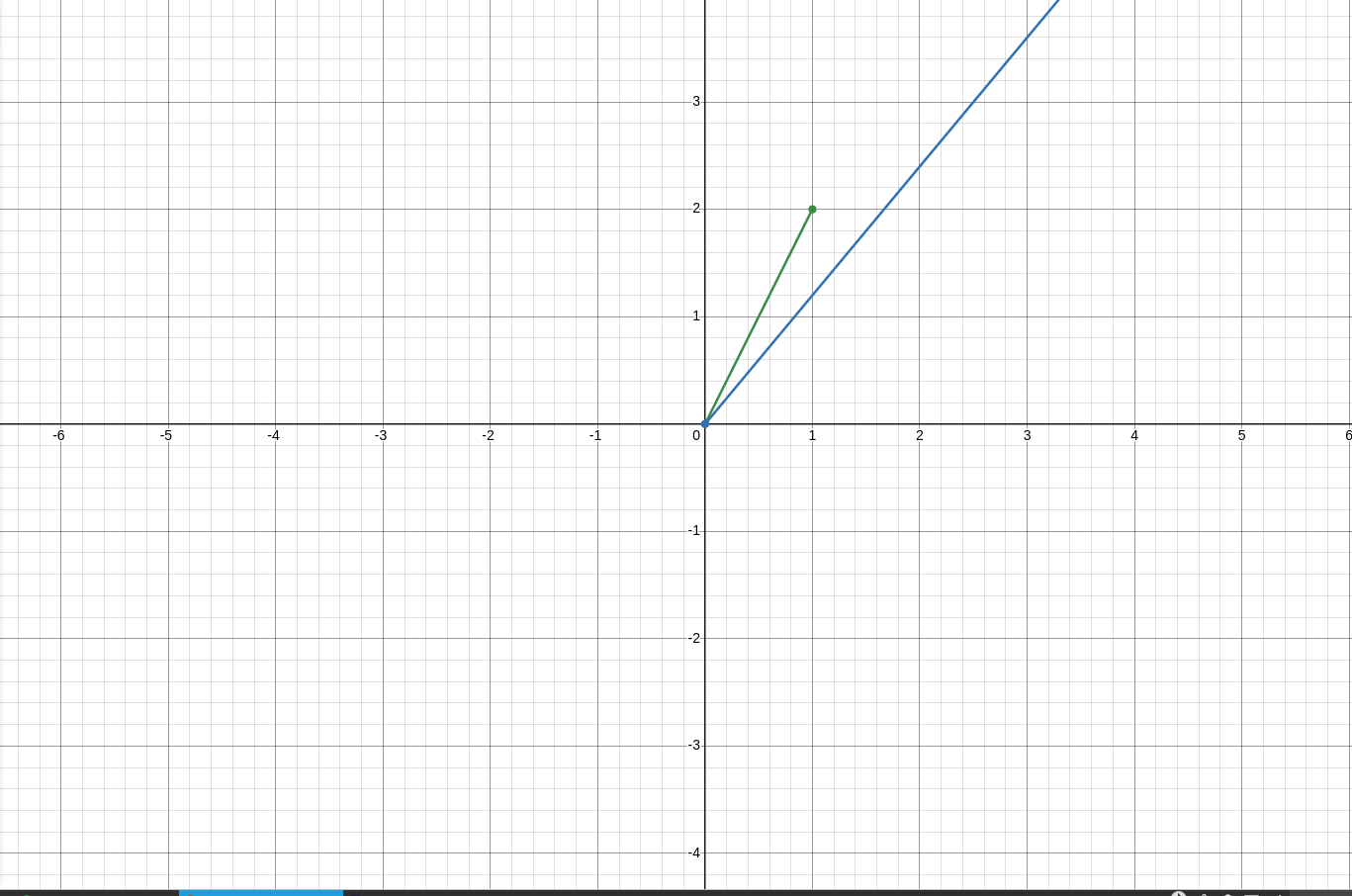
In fact, you can optionally take it a step further to get the approximate angle in degree and see mathematically how small the angle is by taking the arcosine, which is the inverse cosine, of that value. This gets you the value of $\theta$

$\theta = \arccos{.96886} \approx 14.33608 $

Intuitively, we know that an angle of 14 degrees is not very large so by saying that a cosine similarity close to 1 means the two vectors are very similar.

Connecting this to Machine Learning

With this background in the mathematics, let's try to analyze two sentences and turn them into vectors

Sentence A = "The weather is a cold one"

Sentence B = "The weather is on the cold side"

Now let's turn these into vectors and see if we can get a cosine similarity between the two that we can interpret. But notice that if we turned these into vectors, they wouldn't be the same length nor do they have the same words and we wouldn't be able to do the dot product. Well what we can do it take the all of the unique words , make components for each word, and then put a 1 where the sentence has the word and a 0 otherwise.

Sentence	The	weather	is	a	on	the	cold	side	one
A	1	1	1	1	0	0	1	0	1
B	1	1	1	0	1	1	1	1	0

Now, let's get ready to take some cosine similarities. We'll start by getting the magnitude of vector A.

$\begin{Vmatrix} A \end{Vmatrix} = \sqrt{(1)^2+(1)^2+(1)^2+(1)^2+(0)^2+(0)^2+(1)^2+(0)^2+(1)^2} $

Luckily, 1 squared is just 1 and 0 squared is just 0 so it becomes

$\begin{Vmatrix} A \end{Vmatrix} = \sqrt{1+1+1+1+0+0+1+0+1} = \sqrt{6} $

Now we'll get the magnitude of vector B

$\begin{Vmatrix} B \end{Vmatrix} = \sqrt{(1)^2+(1)^2+(1)^2+(0)^2+(1)^2+(1)^2+(1)^2+(1)^2+(0)^2} $

$\begin{Vmatrix} B \end{Vmatrix} = \sqrt{1+1+1+0+1+1+1+1+0} = \sqrt{7} $

6 times 7 is 42 so the denominator for the cosine similarity is $\sqrt{42}$

Now as for the dot product,

$\vec{A} \cdot \vec{B} = (1)(1) + (1)(1) + (1)(1) + (1)(0) + (0)(1) + (0)(1) + (1)(1) +(0)(1) +(1)(0) $

We know that 1 times 1 is 1 and 1 times 0 is 0 so

$\vec{A} \cdot \vec{B} = 1+1+1+0+0+0+1+0+0 = 4 $

So the entire cosine similarity is now this fraction

$\cos{\theta} = \frac{4}{\sqrt{42}} \approx .617214 $

So an interpretation of the cosine similarity tells us that these sentences are similar